

We now carry the 8 over as a remainder to make 81.

15 is larger than 8 and so, we simply write a zero above the 8 because 15 divides into 8 zero times. THe next step is to divide the first digit. The first step is to make a list of the first few multiples of the number being divided by. Draw a line to separate the numbers which passes above the number being divided. To set out long division, write the number being divided by to the left of the number being divided.
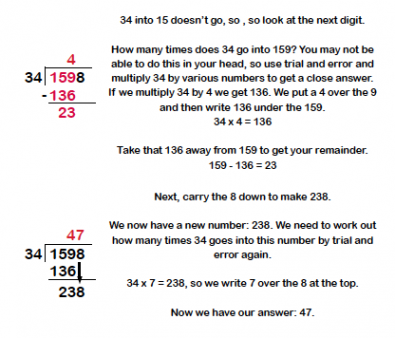
Here is an example of dividing a number using long division step-by-step.
Repeat steps 3 to 5 until there are no more remainders. Write the next digit of the number being divided alongside this remainder. Subtract the largest multiple of the number from the digit being divided to find the remainder. Find the greatest number of times that the number divides into the digit and write this above. Use this list to divide the first digit by this number. Make a list of the multiples of the number being divided by. By showing this level of working out, there is less chance of making a mistake. Long division involves writing out the calculations involved in finding a remainder. The reason we use long division is to provide a structure for dividing by larger numbers. The long division method is used when dividing by a number that has two or more digits. Long division is different from short division in that more working out is shown at each stage in order to calculate the remainders. Try to work through these problems yourself to see if you get the same results.Long division is a method used for dividing by larger numbers. Once you have your answer, do the problem in reverse using multiplication to make sure you got the correct answer.īelow are a few more examples of long division. Double check the problem with multiplication. 
Writing neatly and keeping the numbers lined up can really help you to make fewer mistakes. Make sure you keep all your numbers lined up.
Put a "0" in the left positions of the quotient that you aren't using. Write down a multiple table for the divisor before you start the problem. We also write down 77 underneath the 77 because 7 x 11 = 77.ĥ) Now we subtract 77 from 77. We write down the 7 next to the 1 in the answer area. We now move the 7 down from the end of the 187 (see the picture).Ĥ) In this step we determine how many times 11 will divide into 77. This equals 7, which we write down.ģ) Since we had a remainder of 7, the problem isn't finished. Next, we write 11 underneath the 18 because 1x11 = 11. If we tried 2 that would be 22, which is bigger than 18. In this step, we write down how many times 18 can be divided by 11. The first number "1" is too small, so we look at the first two numbers "18". Let's try a fairly simple example: 187 ÷ 11 = ?ġ) First step is to put the problem into long division format:Ģ) The second step is to determine the smallest number to the left of the dividend, in this case 187, that can be divided by 11. To write this down in long division format it looks like this:








 0 kommentar(er)
0 kommentar(er)
